0x00 卷积神经网络（CNN）

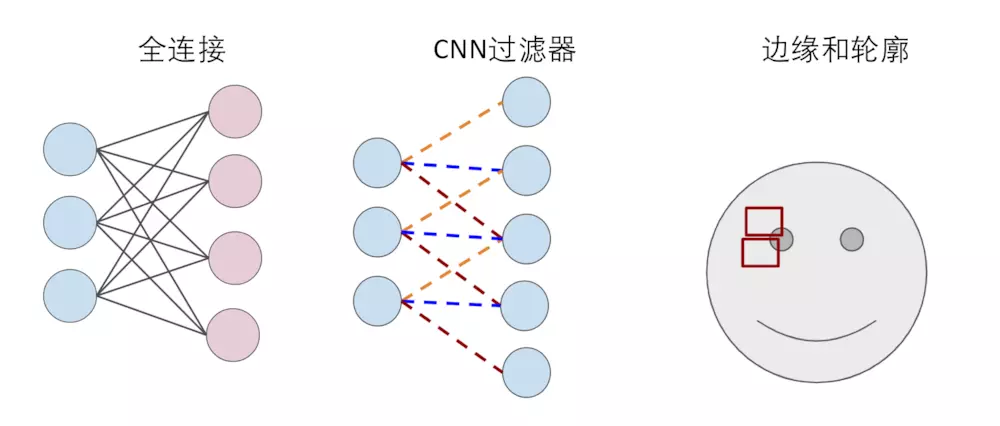
之前介绍的神经网络，每一层的每个神经元都与下一层的每个神经元相连，这种模式称之为全连接（Full Connected）。全连接意味着会产生大量的计算。在上面的例子中，我们可以看到如下代码：

1
2
3
4
5
6
7
8
9
x = tf.placeholder(tf.float32, shape=[None, 784])
y = tf.placeholder(tf.float32, shape=[None, 10])

weight = tf.Variable(tf.zeros([784, 10]))
bias = tf.Variable(tf.zeros([10]))

prediction = tf.matmul(x, weight) + bias

loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y, logits=prediction))

我们发现每一张图片中的784个像素点都与下一层的神经元进行了计算。这种全连接的方法用在图像识别上明显太笨了，因为我们识别MNIST中的数字的话，我们只需要识别数字的轮廓即可，而如何找到数字的轮廓只与当前像素点与其周围的像素点有关。

这个时候卷积神经网络(CNN)就派上用场了，卷积神经网络可以简单地理解为，用滤波器(Filter)将相邻像素之间的轮廓过滤出来，如图：

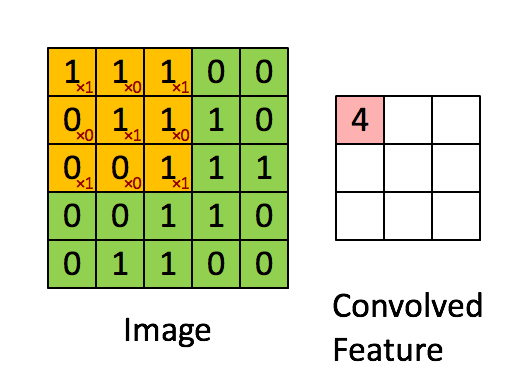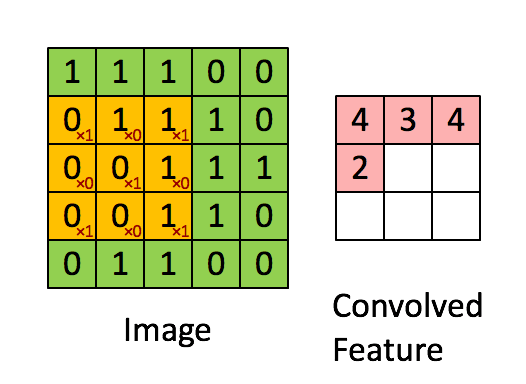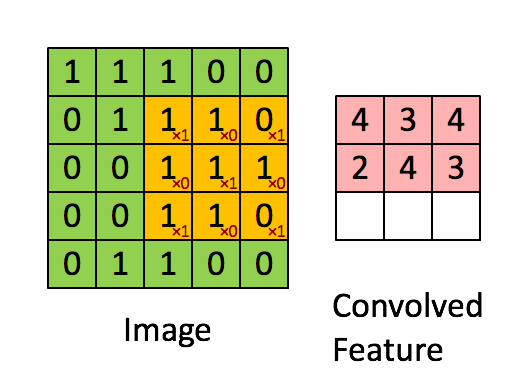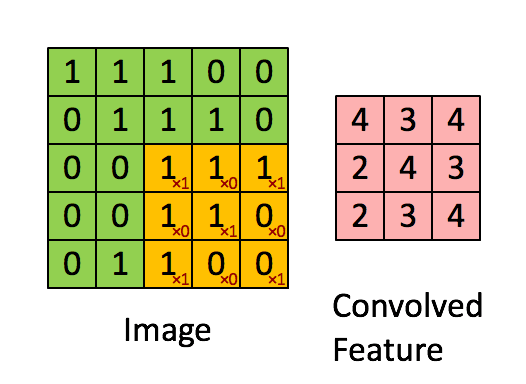
下面我们来详细描述一下卷积的过程。首先我们来看如下动图：

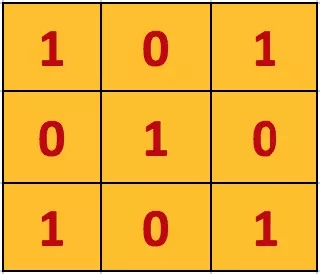
图中有一个黄色的小方块，那个即称为卷积核，他实际的形状实则为一个矩阵：

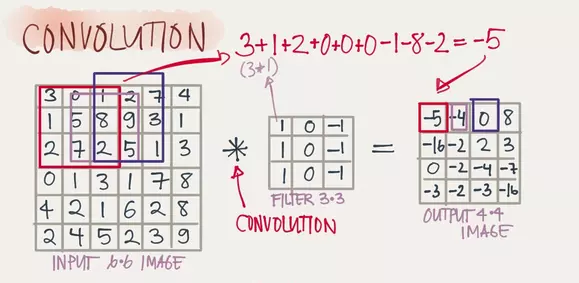
在卷积核走过的过程中，卷积核与覆盖图像的部分进行计算然后得到卷积特征矩阵中某个元素的值，计算方式为卷积核与其覆盖图像的部分每个元素进行乘积然后逐个相加得到最终卷积矩阵元素。如图：

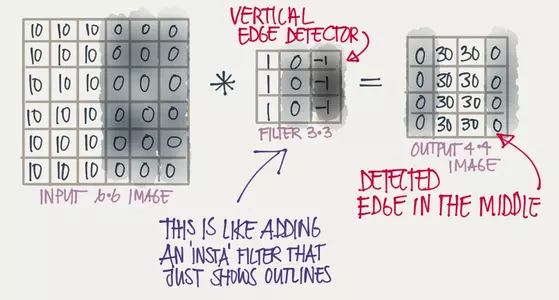
这样做的意义在于可以清晰地划分出图像轮廓，例如在下图中，原矩阵在中间有一条明显的竖直轮廓，轮廓左边是10右边是0，在通过一个3x3的矩阵卷积后得到的结果中，这条轮廓被明显地表示出来了：

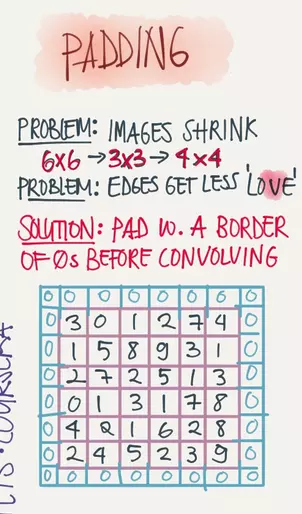
在上面的例子中，一个6x6的输入矩阵在3x3的卷积矩阵的作用下得到的结果是一个4x4的矩阵，如果我们想让结果矩阵和输入矩阵一般大，那我们就需要用到填充（Padding），一般我们使用的方法为SAME Padding，即为在原矩阵外面包裹一层0，如下：

我们再来回顾一下刚才这幅动图：

通过一步步地移动卷积的窗口来完成卷积操作，每次移动的步长即成为stride，步长和padding的大小共同决定了输出层图像的大小。

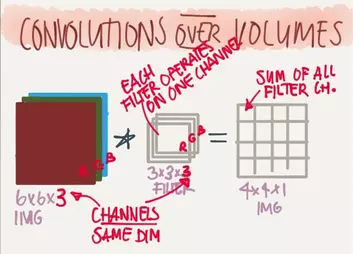
当我们对彩色的训练图片进行处理的时候，所有的色彩都可以由RGB三原色组成，因此我们对彩色图片使用卷积神经网络训练时，往往使用三个通道来对每个颜色进行过滤。于是一个长宽各为6个像素的彩色图片，可以表示为一个6x6x3的3D物体，然后我们使用3x3x3（最后一个3代表通道数）来进行卷积，卷积后将3个通道内的元素相加将其最终合并为1张输出层图片，由此我们将得到一个4x4x1的输出层图片。此时输出层的深度（depth）即为1。如图：

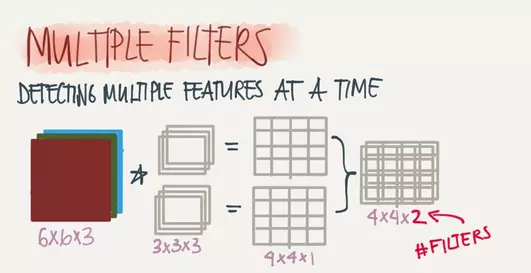
增加卷积核的个数即可增加输出层图片的个数，例如下图中一个6x6x3的输入层图片在2个3x3x3的卷积核的作用下可以得到两个4x4x1的输出层图片。

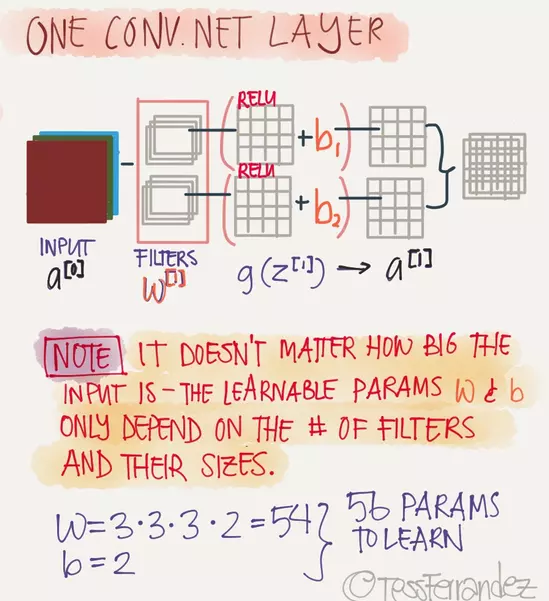
之前我们所创造的全连接神经网络，通常需要一个线性函数(Wx+bWx+b)和一个激活函数共同作用，CNN也是如此，通常在滤波器之后还要加一个激活函数（在图像识别中一般使用Relu函数），CNN中的线性函数同样需要一个权重项W以及一个偏置项b，在CNN中一般使用滤波器的数值作为W，偏置项b一般加在Relu函数之后。如下图所示：

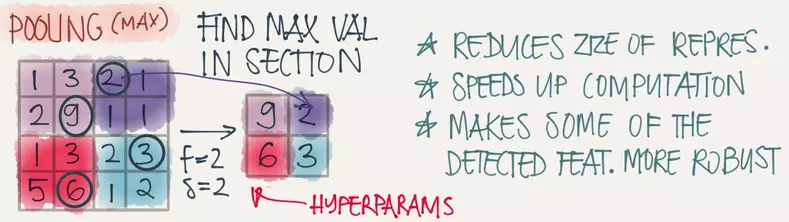
卷积层后面就是池化（pooling）层，池化层主要用于特征降维、压缩数据和参数的数量、加快卷积的速度、减少过拟合，同时提升模型的容错性。池化的方法有很多种，最常用的为max-pooling，即取一个区域的最大值，如图即为将一个4x4的图片max-pooling成一个2x2的图片：

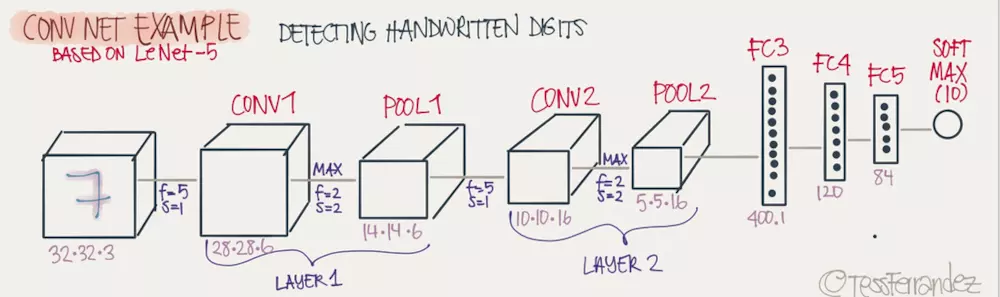
由此，我们有了一个完整的卷积神经网络，其通常有一个或多个的卷积层加池化层，最后再附上几个完整层（Full Connected）构成，如图所示：

0x01 使用CNN训练MNIST

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data

mnist = input_data.read_data_sets("data", one_hot=True)

x = tf.placeholder(tf.float32, shape=[None, 784])
y = tf.placeholder(tf.float32, shape=[None, 10])


# 用于初始化权重
def init_weight(shape):
    res = tf.truncated_normal(shape=shape, stddev=0.1)
    return tf.Variable(res)


# 用于初始化偏差
def init_bias(shape):
    res = tf.constant(shape=shape, value=0.1)
    return tf.Variable(res)


# 定义卷积操作
def conv2d(images, weight):
    # input即为需要计算卷积的图像
    # 形状为[batch, height, width, channels]
    # filter为卷积核形状和input相同，输入一个4D的张量
    # 分别代表[filter_height, filter_width, in_channels, out_channels]
    # out_channels输出通道数等于卷积核个数
    # 步长strides里面的四个参数分别对应输入的images的4个维度的步长
    # SAME padding即为在输入层图片周围补0以使输出层和输入层形状相同
    return tf.nn.conv2d(input=images, filter=weight, strides=[1, 1, 1, 1], padding="SAME")


# 定义最大池化操作
def max_pooling(images):
    # value即为需要池化的对象
    # ksize即为池化窗口的大小，[1, 2, 2, 1]表示池化的四个维度
    # 第一个1即为深度，多少张图片联合起来做池化
    # 第二三个参数即为在一张图片中池化窗口的大小，此处为2x2
    # 第四个参数即为通道数，多少个通道联合起来做池化
    # 我们一般不想在深度和通道数上做池化所以第一四个参数均为1
    # strides即为池化窗口在每一个维度上滑动的步长，参数意义同ksize
    return tf.nn.max_pool(value=images, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding="SAME")


# 将输入图片转化为CNN可用的形状
# shape中的第一个-1用于表示输入图片的数量，如同x shape中的None
# 28, 28, 1用于表示这是一个28x28的图片，有1个通道（因为都是黑白的）
x_image = tf.reshape(x, shape=[-1, 28, 28, 1])

# 卷积核的宽度和高度均为4，第一层输入通道数为1，输出通道数为32
# 将一张图片分为32个特征
con1_weight = init_weight([4, 4, 1, 32])
con1_bias = init_bias([32])
con1 = tf.nn.relu(conv2d(x_image, con1_weight) + con1_bias)
# 对卷积后的结果进行池化
con1_pooling = max_pooling(con1)

# 卷积核的宽度和高度均为4，第二层在第一层的结果上进行卷积
# 第二层输入为第一层的结果，所以输入通道数为32
# 在这一层我们将图片更细分为64个特征
con2_weight = init_weight([4, 4, 32, 64])
con2_bias = init_bias([64])
con2 = tf.nn.relu(conv2d(con1_pooling, con2_weight) + con2_bias)
con2_pooling = max_pooling(con2)

# 展平
# 卷积时我们用了padding，卷积输出的特征图形状与输入图片相同
# 池化时，每个池化窗口的大小为2x2，原先28x28的图片经过两次池化
# 分别变成了14x14最后变成了7x7，最终的输出层有64个通道（特征）
# 所以此处展平时，每张图片最终的表示为7*7*64
# 因为不确定有多少图片，所以第一个维度值设为-1
con_flatted = tf.reshape(con2_pooling, [-1, 7 * 7 * 64])

# 添加1个全连接层
full1_weight = init_weight([7 * 7 * 64, 1000])
full1_bias = init_bias([1000])
full1_train = tf.nn.relu(tf.matmul(con_flatted, full1_weight) + full1_bias)
full1_dropout = tf.nn.dropout(full1_train, rate=0.5)

# 输出层
full2_weight = init_weight([1000, 10])
full2_bias = init_bias([10])
full2_prediction = tf.matmul(full1_dropout, full2_weight) + full2_bias

loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y, logits=full2_prediction))

train = tf.train.AdamOptimizer(learning_rate=0.001).minimize(loss)

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    batch_size = 100
    train_batch_num = mnist.train.num_examples // batch_size
    for _ in range(30):
        for i in range(train_batch_num):
            images, labels = mnist.train.next_batch(batch_size)
            sess.run(train, feed_dict={x: images, y: labels})
        correct_prediction = tf.equal(tf.argmax(full2_prediction, 1), tf.argmax(y, 1))
        accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
        print('========== Iter ' + str(_) + ' ==========')
        # 训练集精确度
        train_acc = 0
        for i in range(train_batch_num):
            images, labels = mnist.train.next_batch(batch_size)
            train_acc = train_acc + sess.run(accuracy, feed_dict={x: images, y: labels})
        print('Train set accuracy: ' + str(
            train_acc / train_batch_num * 100), "%")
        # 测试集精度
        test_acc = 0
        test_batch_num = mnist.test.num_examples // batch_size
        for i in range(test_batch_num):
            images, labels = mnist.test.next_batch(batch_size)
            test_acc = test_acc + sess.run(accuracy, feed_dict={x: images, y: labels})
        print('Test set accuracy: ' + str(
            test_acc / test_batch_num * 100), "%")

最终测试结果，训练集准确率99.89%，测试集准确率99.11%。