查找

0x00 查找

主要有如下查找算法（Searching Algorithms)：

• 顺序查找（Linear Search）
• 二分查找（又称折半查找Binary Search）

以及几个对查找优化的数据类型：

• 哈希表（又称散列表Hash Table）
• B树（参见树那一节）

介绍一个基本概念叫做平均查找长度（ASL）：

ASL的计算公式如下：

$$ASL=\sum_{i=1}^n P_i\times C_i$$

上式中

• n为查找长度
• $P_i$为第$i$个元素为目标的概率
• $C_i$为找到第$i$个元素所需要进行的比较次数

0x01 顺序查找和二分查找

0x00 顺序查找

顺序查找不做详述，就是最简单的查找算法，从第一个开始往后依次查找，直到找到目标或者到达结尾。顺序表一般针对无序的序列。

在此，不给出代码了，仅分析其平均查找长度，对于顺序查找而言在查找成功的情况下，ASL计算为：

$$ASL=\sum_{i=1}^n \frac{i}{n} = \frac{n+1}{2}$$

其中，认为每个元素的查找概率均相同均为$\frac{1}{n}$，当定位目标元素为第$i$个元素时，需进行$i$次比较。

如果查找不成功的话，表中所有的元素都要被比较一次，而且最后还多了一次输入是否到头的比较过程，比较次数即为$n+1$，平均查找长度即为$ASL=n+1$。

顺序查找对表没有任何的要求，可以是顺序表也可是链表，可以有序也可以无序。但是当N较大时，平均查找较长，效率较低。同时对线性的链表只能进行顺序查找。

还要单独说一下有序表的顺序查找，如果在查找之前就知道输入序列有序的话，例如如下输入序列：

1 2 4 5 6 7 8 9

当我要查找元素3时，当查找到第一个比3大的元素时还没有找到3，算法就可以终止了，在此处，当比较到4时，就没必要再继续下去了。这样可以进一步地优化一下查找失败时的平均查找长度：

$$ASL_{查找失败时}=\frac{1+2+3+...+n+n}{n+1}=\frac{n}{2}+\frac{n}{n+1}$$

反正也查不到，那平均到每一次到达失败结点的概率即为$\frac{1}{n+1}$，此处n+1的原因是有n+1个查找失败的顶点，因为我把整个表全部扫描了一遍，我最后还多了一次判断输入是否到头的比较过程。分子最后多了个+n的原因是，当查找进行到输入数据末尾时，由于每一次查找都多了一次比较当前元素是否小于被查找元素的过程，有n个元素，自然也多了n次比较小于的过程。

0x01 二分查找

二分查找又称折半查找，一般用于有序的顺序表。

先从一道LeetCode题目说起，704. Binary Search，这是一道简单题，目的很单纯，就是给你一个顺序表，然后给你一个待查找的元素，让你使用二分查找的方法来查找元素在顺序表中的位置，代码如下：

class Solution {
public:
    int search(std::vector<int>& nums, int target) {
        int lo = 0, hi = nums.size(), mid;
        while (lo < hi)
        {
            mid = (lo + hi) >> 1;
            if (nums[mid] == target)
            {
                return mid;
            }
            else if(nums[mid] > target)
            {
                hi = mid;
            }
            else
            {
                lo = mid + 1;
            }
        }
        return -1;
    }
};

二分查找的过程可以用一棵二叉树来描述，这棵二叉树也被称为判定树，

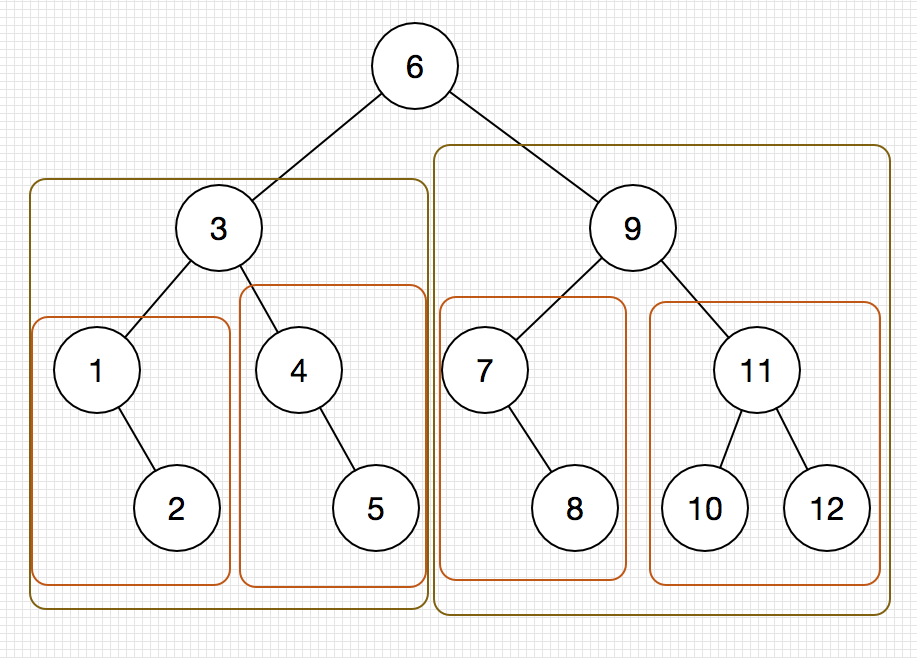
对于一个待查找的输入数列：

1 2 3 4 5 6 7 8 9 10 11 12

我们可以画出其二分查找时的判定树，如下图：

下面来分析一下二分查找的平均查找长度：

由上图可以看出，使用二分查找查找到给定值的时间复杂度不会超过其判定树的高度，所以有：

$$ASL=\sum_{i=1}^h{\frac{1}{n}\times (i\times2^{i-1})} \\ ASL=\frac{1}{n} \times (1\times1+2\times2+...+h\times2^{h-1})\\ ASL=\frac{n+1}{n}\log_2{(n+1)}-1 \\ \Rightarrow ASL\approx \log_2{(n+1)}-1$$

在上式中，h为判定树的高度，当有N个结点时，判定树的高度为：

$$h=\lceil \log_2{(N+1)} \rceil$$

由此可知，二分查找的时间复杂度为$O(\log_2{N})$。

二分查找有一个特点就是需要方便地定位到数列中间的那个位置，所以适合用二分查找的存储结构要具有随机访问的特性，例如数组。因此其并不适用于链表等链式存储结构。

0x02 分块查找

分块查找又称索引顺序查找，可以看为是二分查找和顺序查找的一个整合版本，其基本思想是：

• 将查找表分为若干块，块内的元素可以是无序的，但是块与块之间是有序的，例如第一个块中的最大关键字小于第二个块中的最小关键字，以此类推。
• 有一个索引表，索引表包含了每个块含有的最大关键字，以及第一个起始元素的位置，索引表按关键字有序排列。

分块查找的查找过程分两步，第一步在索引表中确定待查记录所在的块，可以使用顺序查找或折半查找，然后第二步在块内顺序查找。

将索引查找的平均查找长度记为$L_I$，块内查找的平均查找长度记为$L_S$，则ASL有如下计算：

$$ASL=L_I+L_S\\$$

设将长度为n的表平均分为了b块，每块有s条记录，若对索引表使用二分查找时，平均查找长度为：

$$ASL=\lceil \log_2{(b+1)} \rceil+\frac{s+1}{2}$$

若对索引表也使用顺序查找，则平均查找长度为：

$$ASL=\frac{b+1}{2}+\frac{s+1}{2}\\ 代入b=\frac{n}{s}有:ASL=\frac{n+s}{2s}+\frac{s+1}{2}\\ \Rightarrow ASL=\frac{s^2+2s+n}{2s}$$

0x02 哈希表

0x00 基本概念

哈希表（Hash table）又叫散列表，往往被用来实现关联数组（Associative array）。同样可以用来进行快速地查找，其具有以下几个基本概念：

• 散列函数（Hash function）：用于把查找表中的关键字映射成该关键字对应地址的函数，国内教材上一般记为：

  addr = Hash(key); // 通过散列函数Hash得到关键字key的地址Addr

  国外教材上一般写为如下两种形式：

  // 通过散列函数f得到关键字key的地址index
  // 其中散列函数需传入查找表数组的大小array_size
  index = f(key, array_size); 

  或者：

  // 通过散列函数hashfunc得到关键字key所对应的地址hash
  hash = hashfunc(key);
  // 通过这个地址hash与查找表数组大小进行模运算以获取其在查找表的索引地址
  index = hash % array_size;

• 散列表：根据关键字直接访问的数据结构，其建立了关键字和存储地址之间的一种直接映射关系

在理想情况下，对Hash表进行查找的时间复杂度为$O(1)$

再介绍一个概念叫做装填因子（load factor），其计算公式如下：

$$\text{load factor}=\frac{\text{size}}{\text{capacity}}$$

其中，size为哈希表中实际存储的有效元素的个数，capacity为哈希表的容量或者采用拉链法处理冲突时的bucket数组的大小。

在Java10版本实现的HashMap中，默认的装填因子的大小为0.75

0x01 散列函数的构造

构造散列函数时，必需注意如下几点：

• 散列函数的定义域必需包含全部需要存储的关键字，而值域的范围则依赖于散列表的大小或地址范围
• 散列函数计算出来的地址应该能等概率地、离散地、均匀地分布在整个地址空间（discrete uniform distribution），从而减少冲突的发生
• 散列函数应尽量简单，在较短的时间复杂度内算出任一关键字所对应的散列地址

下面介绍集中常用的散列函数：

0x00 直接定址法

就是使用线性函数来计算散列地址：

AddressIndex hashFunc(ElemType key) {
    return a*key + b; // 此处的a和b为常数
}

这种方法快且简单，而且不会产生冲突，仅适合于关键字的分布基本连续的情况，若关键字分布不连续空位较多，那么将会导致大量存储空间的浪费。

0x01 除留余数法

AddressIndex hashFunc(ElemType key) {
    return key % p; // 其中p为质数
}

这同样是一种简单而实用的办法，假定散列表的长度为m，则取小于等于m的最大质数作为p，然后通过取余运算以计算其散列地址。此方法的关键在于质数p的选择，选择一个好的质数p，可以使得每一个关键字都等概率地映射到空间上的任意地址，减少冲突的可能。

0x02 平方取中法

就是取关键字平方值的中间几位作为散列地址。具体取多少位要依实际情况而定，这种方法得到的散列地址与关键字的每一位都有关系，使得散列值分布地比较均匀。适用于关键字的每一位取值都不够均匀或均小于散列地址所需的位数。

0x03 数字分析法

这种方法适合已知关键字的集合，如果更换了关键字就需要重新构造散列函数，在已知关键字集合的情况下，对关键字进行分析，分析每一个关键字中的数字在每一位上的出现频率，然后选取其中数字分布较为均匀的几位作为散列地址。

0x04 折叠法

关键字分割成位数相同的几部分，然后取这几部分的叠加值作为散列值。当关键字中每一位上的分布大致均匀时，可采用折叠法得到散列值

0x02 冲突处理

散列函数都不可能绝对地避免冲突（Collision），当发生冲突时，一般需要再找一个空的Hash地址来存放这个数据，目前有如下几种常用的方法用来解决冲突（collision resolution）。

0x00 开放定址法

开放定址法（Open addressing）指的是可存放新表项的空闲地址即向它的同义词表项开放，又向它的非同义词表项开放，其递推公式如下：

$$Addr_i = (\text{Hashfunc}(key)+d_i)\%m$$

其中m为表长，$d_i$为增量序列，$Addr_i$为计算得出的地址。当确定某一增量序列后，可以采用的处理方法往往是确定的，通常由如下几种方法：

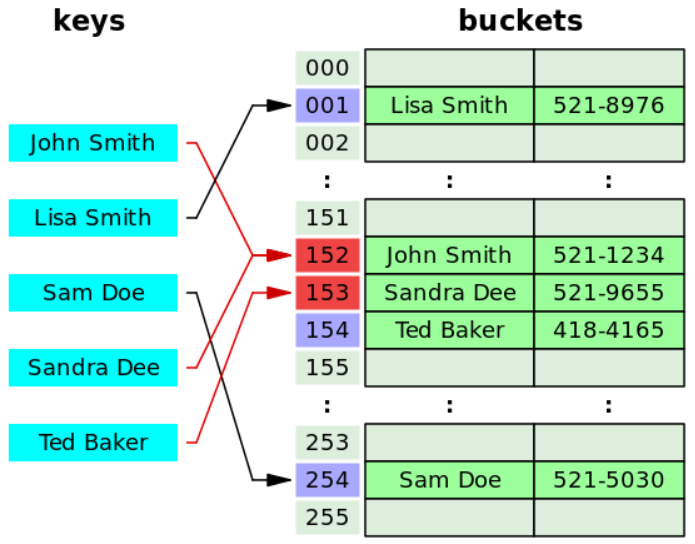
• 线性探测法（Linear probing）：冲突发生时，顺序查看表中的下一个单元，直到找到一个空闲单元把他放进去，如果遇到表尾，那就从表首地址处继续，所以，在表未满的情况下，总能找到一个空闲单元。
  线性探测法可能使第n个散列地址的同义词存入n+1的位置，然后本该存储n+1位置的元素又要去争抢n+2的位置，以此类推，从而会造成大的元素在相邻的散列地址上聚集起来（Primary clustering），降低了查找效率。如下图：

• 平方探测法（又称二次探测法Quadratic probing）：就是当发生冲突时，在原hash地址的基础上加上一个任意的二次多项式（arbitrary quadratic polynomial）以获取新的存储地址。这个二次多项式怎么来呢，下面介绍一下这个算法，当给定一个key值时，我们已经通过hash函数计算出了其hash值为H，但是H位置上已经有元素在占了，如果按照线性探测法，那接下来的判定序列为：

  $$H+1, H+2,...,H+k$$

  如果使用平方探测法，接下来的判定序列即为：

  $$H+1^2, H+2^2,...,H+k^2$$

  其中$k \leqslant \frac{m}{2}$，且散列表的长度m必需是一个可表示成4k+3的素数。
  别看仅仅在线性探测的序列上对增量加了个平方，这却有效地缓解了线性探测中失效后元素的聚集问题（clustering problem）。
  它的缺点在于不能探测到散列表上的所有单元，但至少能探测到一半的单元。
  这种方法被用于Unix文件系统（Unix File System又称Berkeley Fast File System）用于分配新的空闲块。

• 再散列法（Double hashing）：此种方法需要使用2个散列函数，当第一个散列函数计算出来的地址值发生冲突时，再由第二个散列函数计算该关键字的地址增量。其具体的散列函数形式如下：

  $$Addr_i = (\text{Hash}_1(key)+i\times \text{Hash}_2(key))\%m$$

  上式中的$i$为冲突发生的次数，初始为0，再散列法中，最多经过m-1次探测就会遍历表中所有的位置回到$Addr_0$的位置。

在开放定址的情形下，不能随便物理删除表中已有元素，因为删除元素将会截断其他具有相同散列地址元素的查找地址。所以若想删除一个地址，需要给它做一个删除标记，在逻辑上删除，这样做的副作用是在执行多次删除后，表面上看起来散列表很满，实际上有许多位置没有利用，因此需要定期维护散列表，把带有删除标记的元素物理删除。

同时，即便使用一个良好的hash函数，使用开放定址法进行冲突处理的hash表的查找性能也会随着装填因子的升高而降低。

0x01 拉链法

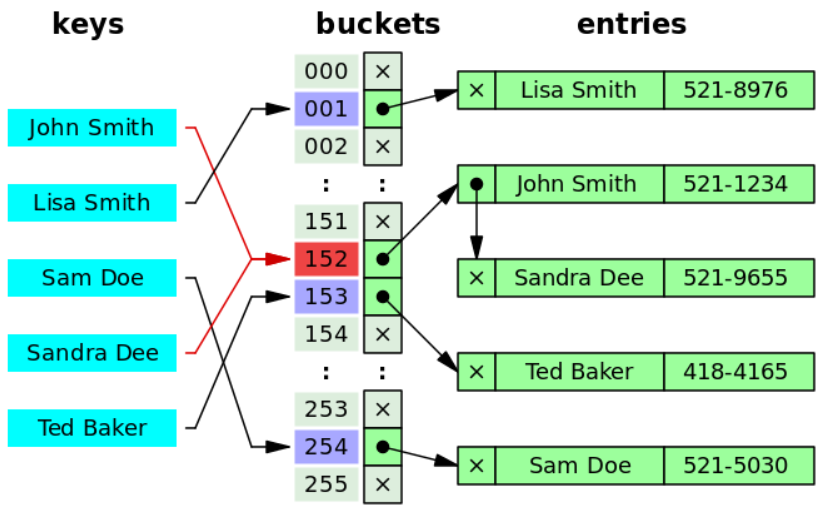
我们可以把所有同义的关键词全部存储到一个线性链表中，这个线性链表由其散列地址唯一标识，这种处理冲突的方法称为拉链法（Separate chaining）。因为查找、删除、插入操作都在同义词链中进行。所以拉链法往往适用于经常插入和删除的情况。如图：

一个设计优良的hash表使用拉链法来解决冲突，每一个bucket应含有0个或1个链表项（entries），有时可能出现2-3个，再多的情况下就很少出现了。

一定要注意在拉链法中，hash表是一个存放指针的数组

0x03 性能分析

哈希表的查找过程与其构造过程基本是一致的：

• 首先通过散列函数通过查找的关键字计算出其散列地址
• 然后查找表中相应地址是否存在元素，若没有则查找失败，若有则比较其与被查找的值是否相同，若相同则返回查找成功的标识，若不相同则执行下一个步骤
• 使用哈希表给定的冲突处理的方法来计算下一个散列地址，然后转入上一个步骤继续执行

哈希表的查找效率往往取决于三个因素：散列函数、处理冲突的方法以及装填因子

哈希表的平均查找长度依赖于散列表的装填因子，装填因子越大，哈希表就越满，发生冲突的可能性就越大。虽然哈希表在关键字与记录的存储位置之间建立了直接的映像，但是由于冲突的产生，使得哈希表的查找仍然是一个给定值与关键字比较的过程。哈希表查找的平均时间复杂度为$O(1+\text{load factor})=O(1)$，在最坏情况下，采用拉链法处理冲突时装填因子是有可能大于1的，这样时间就消耗在了遍历这个链表上，此时的时间复杂度为$O(N)$。同样采用开放定址法处理冲突，当hash函数始终返回一个固定的地址值，但是这个地址值存储的元素又不为所需查找的元素时，也需要依次地向下遍历直到找到元素，最坏的情况下，遍历一周再回到hash地址值前一个，所需的最坏时间复杂度仍为$O(N)$。

0x03 字符串的模式匹配

0x00 暴力破解

暴力破解的过程不用多说了吧，直接上一道LeetCode题目练习一下

28. Implement strStr()

这道题的目的很单纯，就是让我们实现一下strstr函数，在此环节，我们首先使用暴力破解的方式求解此题，代码如下：

class Solution {
public:
    int strStr(std::string haystack, std::string needle) {
        if (needle.size() == 0)
        {
            return 0;
        }
        if (haystack.size() >= needle.size())
        {
            for (int i = 0; i < haystack.size() - needle.size() + 1; ++i)
            {
                if (haystack[i] == needle[0])
                {
                    int j = 0;
                    for (; j < needle.size(); ++j)
                    {
                        if (haystack[i + j] != needle[j])
                        {
                            break;
                        }
                    }
                    if (j == needle.size())
                    {
                        return i;
                    }
                }
            }
        }
        return -1;
    }
};

这道题的测试数据其实并不是很好，因为这道题使用暴力破解和使用KMP算法居然一样快，提交上去之后都是超过100%的人，没有明显的区分。

此题有一个地方需要注意，在它题目的Clarification里面也写明了：

Clarification:

What should we return when needle is an empty string? This is a great question to ask during an interview.

For the purpose of this problem, we will return 0 when needle is an empty string. This is consistent to C’s strstr() and Java’s indexOf().

如果在面试的时候被面试官问到这个问题，一定要专门地问问你的面试官当模式串needle为空的时候，应该怎么处理呢？

在C语言的strstr函数的实现以及Java的String类的indexOf函数实现中，当模式串为空时，应返回0。

暴力破解的时间复杂度在很多国内教材上写的都是$O(N\times M)$，其中的$N$和$M$是主串和模式串的长度。

但是我们可以适当地对其进行缩减，就比如说上述代码中，我们可以在遍历主串查找时当i == haystack.size() - needle.size() + 1时就跳出循环，因为此时主串已经比匹配串短了，后面的一定不可能匹配成功了，我们也没有必要再进行下去了，所以此时的时间复杂度为$O(\min{(N,M)}^2) \leqslant O(N\times M)$。

0x01 KMP算法

KMP算法（KMP algorithm）的全称是三个人的名字，是一种改进后的字符串模式匹配算法，可以在$O(N+M)$的时间复杂度上完成操作。这个算法不是很好理解，先来看个视频预热一下：

KMP Algorithm | Searching for Patterns | GeeksforGeeks

显然，我看完这个视频还是一点没懂，维基百科的解释也不是很好理解，尤其是对那个m更是不知所云，KMP algorithm，但是仍然推荐大家都看一下。后来又看了一篇文章：

The Knuth-Morris-Pratt Algorithm in my own words

这篇文章写得真是很好，文章开头几句话就反应了我的心声

For the past few days, I’ve been reading various explanations of the Knuth-Morris-Pratt string searching algorithms. For some reason, none of the explanations were doing it for me. I kept banging my head against a brick wall once I started reading “the prefix of the suffix of the prefix of the…”.

在过去的几天了我读了若干种有关KMP算法的解释，出于某些原因，我仍然不懂，大脑依旧爆炸…

所以说，按文章所说，让我们坐下来（sit down），用一些例子（do a bunch of examples），把他们都复盘出来（diagram them out）：

按一般的教材中呢，它肯定会先介绍KMP算法中的Partial Match Table，这个玩意在国内的教材中一般写作next数组，我们先抛开他，先看算法的流程：

我要在S里面寻找W，其中S和W如下：

S: bacbababaabcbab
W: abababca

我们先给定这个Partial Match Table，稍后再讲其求解过程：

char:  | a | b | a | b | a | b | c | a |
index: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 
value: | 0 | 0 | 1 | 2 | 3 | 4 | 0 | 1 |

在这个表里面呢，第一行是模式串，第二行是表的索引下标，第三行为部分匹配值。

首先比较字符串S的第一个字符与W的第一个字符，两者不匹配，我们把搜索词W往后移一位：

S: bacbababaabcbab
    |-
W:  abababca

这个时候我们发现S中的a和W中的a匹配了，我们再看其下一个，下一个就不匹配了，在上图中，我用-标记了出来，此时W中的最后一个匹配字符为正数第一个a，我们查表可得，其部分匹配值为0，此时，不需要跳过任何字符，向下走一个：

S: bacbababaabcbab
W:   abababca

S中的c和W中的a并不匹配，再往下走一个，依次重复此过程，直到走到了a：

S: bacbababaabcbab
       |||||-
W:     abababca

我们这个时候发现呢，部分匹配已经匹配成功了W的前5个字符ababa，最后一个正确匹配的元素时W的正数第5个字符a，查表可知其部分匹配值为3，然后算出其需要向下移动的位数：

移动位数 = 已匹配的字符数 - 对应的部分匹配值

在此处，已经匹配了5个字符，部分匹配值为3，所以向下移动的位数为5-3=2，在下图中，我使用x代表跳过的字符：

S: bacbababaabcbab
       xx|||-
W:       abababca

现在我们发现有3个匹配的，即aba，最后一个匹配的字符为正数第3个a，查表得知其部分匹配值为1，向下移动的位数为3-1=2，所以再向下移动2位：

S: bacbababaabcbab
         xx|-     -
W:         abababca

我们现在发现了一个问题，就是模式串W的长度已经比主串S剩余的长度要多了，注意上图中最后的那个小-，至此算法结束，没有找到匹配项。

好，现在让我们说一个让大家都头疼的问题，就是那个Partial Match Table到底是怎么生成的呢？这个曾经也是我的main obstacle between me and understanding KMP（理解KMP算法的主要障碍）。

这个Partial Match Table只跟需要查找的模式串有关，跟主串是无关的，在上例中我们需要查找的模式串W为abababca，模式串有8个字符，那么Partial Match Table长度也跟着为8，我们先来了解2个概念，一个叫Proper prefix一个叫Proper suffix：

• Proper prefix（前缀）：就是除了最后一个字符外，一个字符串的所有头部组合（cut off），就比如说Snape，它的Proper prefix就有S, Sn, Sna, Snap这样。
• Proper suffix（后缀）：就是除去第一个字符外，一个字符串全部的尾部的组合（cut off），就比如说单词agrid，它的Proper suffix就有grid, rid, id, d这样。

TL;DR

不好意思，我实在不知道Proper prefix和Proper suffix在中文里应当怎么翻译，我读了一些国内的教材也没有给出相应的答案，有的书中将其直接称呼为前缀和后缀，我觉着这样是不合适的，如果是这样的话，前面的proper就完全没有表达出来，邓俊辉老师的书将其翻译为真前缀真后缀，这样就显得太晦涩。王道的教材中直接将Longest proper prefix称之为最长公共前缀，把proper译成公共的，这样其实是不合适的，最长公共前缀应该叫Longest common prefix，我还在LeetCode上做过这个题呢。所以在此处我直接用英文来代表这个东西。

我们在此处姑且将Proper prefix和Proper suffix称之为前缀和后缀

好，我们现在知道了啥叫Proper prefix和Proper suffix，我们现在就开始吧，求解模式串abababca的Partial Match Table：

• a的前缀和后缀均为空，共有的元素长度为0
• ab的前缀为a，后缀为b，共有的元素长度为0
• aba的前缀为a, ab，后缀为ba, a，两者共有的元素仅有a长度为1
• abab的前缀为a, ab, aba，后缀为bab, ab, b，两者共有的元素仅有ab其长度为2
• ababa的前缀为a, ab, aba, abab，后缀为baba, aba, ba, a，两者共有的元素有aba和a，最长公共元素为aba，长度为3
• ababab的前缀为a, ab, aba, abab, ababa，后缀为babab, abab, bab, ab, b，最长公共元素为abab，长度为4
• abababc的前缀为a, ab, aba, abab, ababa, ababab，后缀为bababc, ababc, babc, abc, bc, c，没有一个相同的，共有的元素长度为0
• abababca的前缀为a, ab, aba, abab, ababa, ababab, abababc，后缀为bababca, ababca, babca, abca, bca, ca, a，最长公共元素为a，长度为1

然后将其最长公共元素的长度与其在字符串中的下标关联起来即形成了Partial Match Table，如下：

char:  | a | b | a | b | a | b | c | a |
index: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 
value: | 0 | 0 | 1 | 2 | 3 | 4 | 0 | 1 |

第一行为搜索串W，第二行为搜索串W其中的各个元素的下标，第三行即为我们通过上述步骤求得的最长公共子串的长度

KMP算法的时间复杂度为$O(N+M)$，但是在一般情况下，使用暴力破解的时间复杂度也基本近似$O(N+M)$，这也是为什么在LeetCode题目28. Implement strStr()下使用暴力破解和KMP算法求解的运行时间都可以超过100%的人的原因。KMP算法往往适用于主串与子串有很多部分匹配的时候，这样才能显得KMP算法比暴力破解快很多，因其主要的优点就是主串不回溯。

终于我知道next数组是怎么求出来的了，但是求解next的数组的那个代码实现算法，反正我第一遍没看懂，确实有点让人丈二和尚摸不着头脑，一脸懵逼，不怕，慢慢来，我们再来复盘一下：

next数组其实还有一种求法，就是模式串对自身进行匹配运算，在任一位置往前能够匹配的最大长度即为当前的next数组的值，还是给定模式串abababca记为S，我们从next[1]看起，模式串对自身进行匹配运算，此时b和a不相等，能匹配的最长长度为0，所以next[1]=0

 i
 |
abababca      next[1] = 0
 abababca
 |
 j

再往下走一个，此时在位置i处，a和a相等匹配了，在下面那个模式串中j前面只有a这么一个是正确匹配了的，所以next[2]=1

  i
  |
abababca      next[2] = 1
  abababca
  |
  j

按照常规的匹配算法，第一个匹配了，那就定住模式串去检验模式串的下一个，让j往下走一个，我们发现b又匹配了，这个b之前还有1个a也是匹配成功了的，所以next[3]=2：

   i
   |
abababca      next[3] = 2
  abababca
   |
   j

依次向下，陆续有：

    i
    |
abababca      next[4] = 3
  abababca
    |
    j

     i
     |
abababca      next[5] = 4
  abababca
     |
     j

到了如下图的这个位置，开始出现了失配，如下：

      i
      |
abababca      
  abababca
      |
      j

这个时候我们移动下面的那个模式串，此时c和a失配了，所以next[6]=0 ：

      i
      |
abababca      next[6] = 0      
      abababca
      |
      j

在往下移动一格，得出next[7]：

      i
      |
abababca      next[7] = 1      
       abababca
       |
       j

这样，我们即可得出如下求解next数组的方法，代码如下：

void getPartialMatchTable(std::string& needle, 
                          std::vector<int>& next)
{
    int i = 0;
    int j = -1;
    next[0] = -1;
    while (i < needle.size() - 1)
    {
        if (j == -1 || needle[i] == needle[j])
        {
            next[++i] = ++j;
        }
        else
        {
            j = next[j];
        }
    }
}

对题目28. Implement strStr()使用KMP算法的代码如下：

class Solution {

    void getPartialMatchTable(std::string& needle, std::vector<int>& next)
    {
        int i = 0;
        int j = -1;
        next[0] = -1;
        while (i < needle.size() - 1)
        {
            if (j == -1 || needle[i] == needle[j])
            {
                next[++i] = ++j;
            }
            else
            {
                j = next[j];
            }
        }
    }
public:
    int strStr(std::string haystack, std::string needle) {
        if (needle.size() == 0)
        {
            return 0;
        }
        std::vector<int> next(needle.size());
        getPartialMatchTable(needle, next);

        int i = 0;
        int j = 0;
        int hs = haystack.size();
        int ns = needle.size();

        while (i < hs && j < ns)
        {
            if (j == -1 || haystack[i] == needle[j])
            {
                ++i;
                ++j;
            }
            else
            {
                j = next[j];
            }
        }
        return j == needle.size() ? i - j : -1;
    }
};

在写这段代码的时候发生了一段小插曲，一开始的时候，我是这样构造那个while循环的：

while (i < haystack.size() && j < needle.size())
    ... omitted ...

上面的代码是错的，你发现这样错在哪了吗？把上述代码改成下面这样就对了：

int hs = haystack.size();
int ns = needle.size();
while (i < hs && j < ns)
    ... omitted ...

这个错误很隐蔽，以至于找到然后修改这个错误花费了我将近一个小时的时间，直到我看到了编译器给我返回的警告我才恍然大悟：

Warning	C4018    '<': signed/unsigned mismatch

看到这个警告突然有种被狗日了的感觉涌上心头，std::string的size函数返回的是size_t类型的值啊，size_t是unsigned，前面的i和j是signed，而且还有可能等于-1啊，当i=-1的时候，我们先假设此时的size函数返回的值为5，当i=-1的时候，就会发生如下比较：

int(-1) < unsigned(5)

比较的过程中，int类型的值将会被自动地转换成unsigned类型，一个负数-1转换成无符号整数unsigned类型会发生什么呢，这个数会变成UINT_MAX - 1啊，于是上述比较就会返回false，-1就这么顺理成章地大于5了！

以后再也不敢不看编译器警告了。