0x00 导言

文章地址：Science Direct

我的批注版地址：Commented Paper

这篇文章旨在解决图像检索问题中以子图搜全图的问题。

0x01 背景知识

0x00 VLAD

VLAD算法的简介可简单参考这篇论文的2.1小节All about VLAD。

VLAD是一个比较老的图像特征提取算法，过程也相对简单：

  1. 首先需要在训练图片数据集上训练一个码表（codebook），词表的训练方法为：对训练集中的图像提取d维的SIFT特征，然后将所有图像的所有SIFT描述子汇总在一块，使用K-means算法去做一个聚类，然后将所有聚类的中心点组合为一个码表。其中K的选择一般为64或256。在此步，我们可以将提取出的SIFT兴趣点记为x=(x1,x2,⋯ ,xn)x=(x_1, x_2,\cdots, x_n)，同时将训练好的码表记为Cvlad=(c1,c2,⋯ ,cK)C_{vlad}=(c_1, c_2, \cdots, c_K)，其中K为聚类中心点的个数。

  2. 对于一张新来的图像，首先也是提取它的SIFT特征，然后将这张图像所有的SIFT描述子根据最邻近原则分配到我们在步骤1中提取到的词表中；

  3. 计算这张图片SIFT描述子与它们所分配到词表的聚类中心点的残差和（即：两向量相减所得的差），这样我们就能得到一个长度为k×dk\times d的未归一化的VLAD特征向量。公式化的表述如下：

    Vk=∑i:NN(i)=k(xi−ck)V_k=\sum_{i:NN(i)=k}(x_i-c_k)

  4. 对上述向量实施归一化，归一化的过程分为两步：

    1. 首先进行Power-law Normalization，说白了就是引入一个介于区间[0, 1)上的常数α\alpha，然后在保留原始符号的情况下，对原始向量中的每一项的绝对值做α\alpha次方运算，即：V=sign(V)∣V∣αV=sign(V)|V|^\alpha
    2. 此后对上一步的结果实施L2归一化，即为：V=V∣∣V∣∣2V=\frac{V}{||V||_2}

经过上述步骤，我们就得到了一个大小为1×(k×d)1\times (k\times d)的VLAD向量。

注：

有文章指出使用SURF算法替代上述的SIFT可以取得更好的检索效果及更快的检索速度。

0x01 Scalable Overlapping Partition algorithm (SOP)

这是一个图像分区的算法，用来将原始图像按一定规则分割为多个不同子图（block），如下是分区流程：

  1. 原始图像本身作为一个整体的block；
  2. 1x原始图像宽度，12\frac{1}{2}x原始图像高度，以14\frac{1}{4}x原始图像高度为步长做滑动窗口自上而下滑动，可得3张子图；
  3. 12\frac{1}{2}x原始图像宽度，1x原始图像高度，以14\frac{1}{4}x原始图像高度为步长做滑动窗口自左而右滑动，可得3张子图；
  4. 12\frac{1}{2}x原始图像宽度和12\frac{1}{2}x原始图像高度，以14\frac{1}{4}x原始图像高度作为步长的滑动窗口，自上而下自左而右滑动，可得9张子图；
  5. 14\frac{1}{4}x原始图像宽度和14\frac{1}{4}x原始图像高度，以18\frac{1}{8}x原始图像高度作为步长的滑动窗口，自上而下自左而右滑动，可得49张子图；

上面这一套流程下来，由一张原始图片，我们就得到了65张子图。

0x02 主要贡献

  1. SIFT和SURF算法所计算出来的图像特征描述子，只关注了梯度特征而忽略了颜色特征，本文对二者做了一个结合，提出了一种新型的复合描述子SURFCN，这使得提取出来的特征具有更强的区分性。最终，这个组合特征将被编码为一个VLAD矩阵。
  2. 为了实现基于子图的图像检索，本文把上述VLAD矩阵与用于表述空间信息的神经特征做了一个结合，这个结合体我们称之为视觉短语（visual phrase）。
  3. 在检索阶段，我们会对每个图像的子图创建子图索引（block index）。检索时，我们会同时考虑词汇表的相似度和子图的相似度。

0x03 方法论

0x00 简介

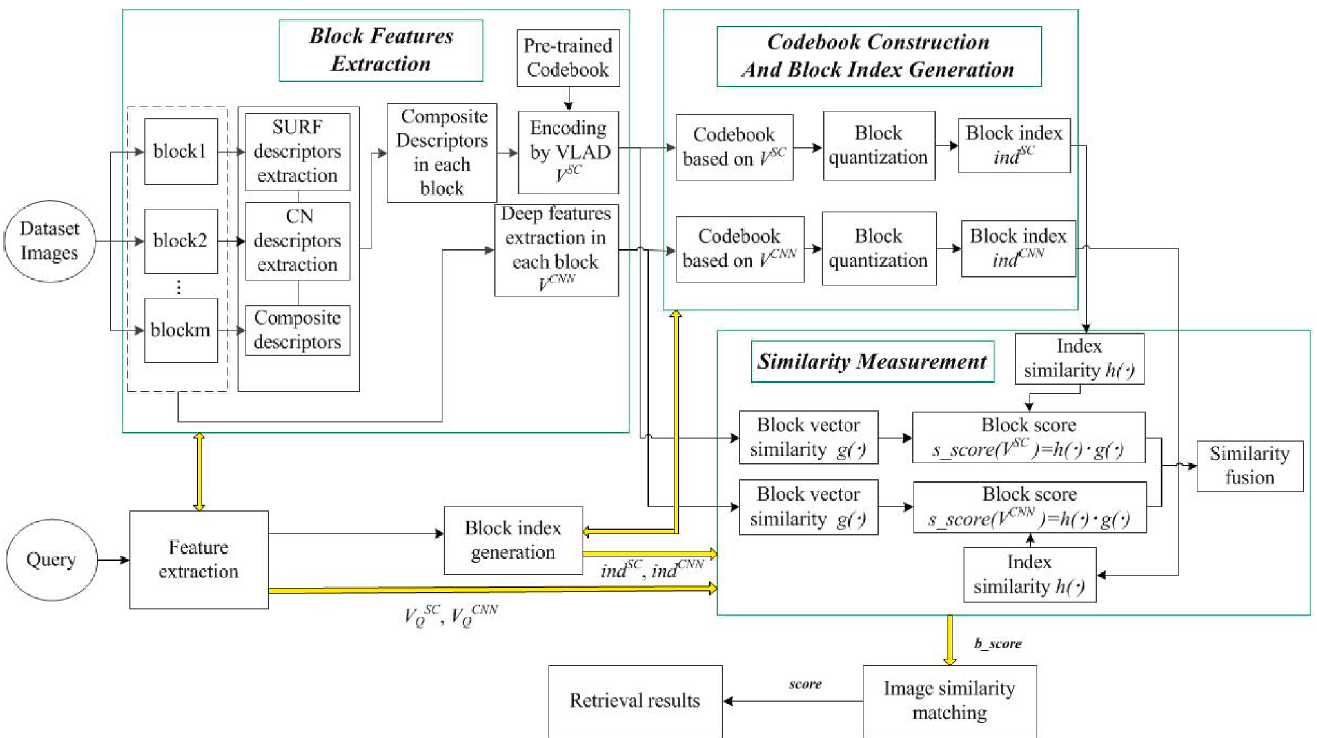
如上图所示，整个流程将分为如下三个模块：

  1. 块特征提取（Block features extraction）：首先使用SOP算法对输入图像进行分区，然后对每个分区提取它们的SURF描述子以及CN（Color Names）描述子，然后再将SURF描述子和CN描述子进行一个整合，整合后的结果称之为组合描述子（Composite Descriptor）。最终将这个组合描述子使用一个VLAD模型将其编码为一个向量。同时，提取每个分区的深度特征。这些共同构成这个子图的块特征（Block Feature）。
  2. 构建码表和块索引（Codebook construction and block index generation）：在训练数据集上，依据VLAD模型编码后的组合描述子和深度特征，使用k-means聚类算法，分别构建两个码表。然后再将新来图片的块特征分配到码表中与之最近的词汇上。
  3. 基于块的相似度测量（Block-based similarity measurement）：根据块索引的相似度与块特征的相似度计算一个块匹配度（block matching score），一张图片所有子图的块匹配度就是这张图片与目标图片的匹配程度。

0x01 组合描述子（Composite Descriptor）

组合描述子在计算的时候会同时考虑它的梯度特征和颜色特征，梯度特征使用SURF算法来进行提取，颜色特征则使用CN描述子来进行表述。我们基于如下3点考虑选择了CN描述子：

  1. CN描述子与颜色的色度（shade）无关，也就是说，对于同一个颜色的不同色度，其计算出的描述子的值是相同的。深红和浅红就是同一种颜色的两种不同色度。
  2. CN描述子可以用来表示无彩色（achromatic color），无彩色指除了彩色以外的其它颜色，常见的有黑、白、灰。明度从0变化到100，而彩度很小接近于0。
  3. CN描述子是一种紧凑表示，也就是说占用的空间很少。

对于一张图片II，我们首先提取它的SURF描述子，记为xSURF=(x1SURF,x2SURF,⋯ ,xnSURF)x^{SURF}=(x^{SURF}_1, x^{SURF}_2, \cdots, x^{SURF}_n)，其中n为所提取出的SURF描述子的个数，对于其中任一SURF描述子xiSURFx^{SURF}_i，我们以其为中心做一个p×pp\times p的正方形，然后提取这一区域内所有像素的CN描述子，然后我们计算这些CN描述子向量的均值作为这一区域的CN描述子向量。然后对于n个SURF描述子，我们就有了与之对应的n个CN描述子，将其记为xCN=(x1CN,x2CN,⋯ ,xnCN)x^{CN}=(x^{CN}_1, x^{CN}_2, \cdots, x^{CN}_n)。此后，我们引入两个权重系数ω1,ω2\omega_1, \omega_2来将如上两个向量前后相接拼起来，得：xiSC=[ω1xiSURF;ω2xiCN]x^{SC}_i=[\omega_1x^{SURF}_i;\omega_2x^{CN}_i]，其中，我们在设置这两个权重系数时，我们使ω1+ω2=1\omega_1+\omega_2=1。这样，我们假设dSURFd^{SURF}为SURF描述子的维度，dCNd^{CN}为CN描述子的维度，那么对于其中某一个组合描述子xiSCx^{SC}_i的维度即为dSC=dSURF+dCNd^{SC}=d^{SURF}+d^{CN}。

0x02 块索引（Block Index）

对于一张图片，我们首先将其分成S个block，对于其中的一个block s，我们提取其组合描述子，并将其记为x(s)SC=(x1SC,x1SC,⋯ ,xnsSC)x_{(s)}^{SC}=(x_1^{SC}, x_1^{SC}, \cdots, x_{n_s}^{SC})，然后我们再将所有的组合描述子x(s)SCx_{(s)}^{SC}使用VLAD算法进行编码，并将其结果记为V(s)SCV_{(s)}^{SC}。此外，我们还会对这张图片整体提取其深度特征，并记为V(s)CNNV_{(s)}^{CNN}。我们首先对训练集中的所有图片，提取上述的2种特征，此后使用K-means算法将其聚合到k个类别中。然后使用K-means的聚类中心点组成我们的词汇表（codebooks，码表），对于这个训练数据集中所有图像的组合特征向量VSCV^{SC}和深度特征向量VCNNV^{CNN}，我们就可以将其所对应的全体的聚类中心记为CSC∈RdSC×kC^{SC}\in R^{d^{SC}\times k}和CCNN∈RdCNN×kC^{CNN}\in R^{d^{CNN}\times k}。

对于某一张图片s的组合特征向量V(s)SCV_{(s)}^{SC}和深度特征向量V(s)CNNV_{(s)}^{CNN}，我们就可以计算出它们与码表中所有聚类中心点的距离，并选出与之距离最近的m个（m≪km \ll k）聚类中心点（记为：(i1,i2,⋯ ,im)(i_1, i_2, \cdots, i_m)）在码表中的索引作为对特征向量V(s)SCV_{(s)}^{SC}和V(s)CNNV_{(s)}^{CNN}的索引向量，也就是块索引，并将其记为ind(s)SC∈R1×mind_{(s)}^{SC}\in R^{1\times m}与ind(s)CNN∈R1×mind_{(s)}^{CNN}\in R^{1\times m}。

R1×mR^{1\times m}的原因是m个聚类中心，每个聚类中心用一个数字来进行标号。

这么做的主要意图如下：

其一，降低检索时间。在检索的过程中，我们会首先提取待检索图片与数据库中目标图片的块索引，然后判断二者是否有交集。如果没有的话，那就是完全不相似，并且在此次检索过程中应该被筛除掉。论文作者在Holidays dataset中试验，发现这一步可以在检索过程中预先筛掉15%的图片。

其二，可以对仅使用图像特征检索的结果做一个加强，去掉一些被图像特征检索错误召回的图片。

0x03 相似度评价（Similarity Measurement）

假设现在有2张图片I1I_1和I2I_2，将其切分为S个子图后的图像表示为VI1=[VI1(1),VI1(2),⋯ ,VI1(S)]V_{I_1}=[V_{I_1(1)}, V_{I_1(2)}, \cdots, V_{I_1(S)}]以及VI2=[VI2(1),VI2(2),⋯ ,VI2(S)]V_{I_2}=[V_{I_2(1)}, V_{I_2(2)}, \cdots, V_{I_2(S)}]。其中的每一项都是每一个block的特征，如果写成VI1(1)SCV_{I_1(1)}^{SC}就可以表示第一张图片第一个block的SURFCN特征，以此类推，VI1(1)V_{I_1(1)}即为第一张图片第一个block的组合特征。为了提高相似判断的准确率，我们使用块索引和特征向量的组合相似度来进行相似性评价。对于两张图片内的两个block，我们使用如下公式来计算其相似度（similarity score）：

s_score=h(CindI1(s),CindI2(s))⋅g(VI1(s),VI2(s))\text{s\_score}=h(C_{ind_{I_1(s)}}, C_{ind_{I_2(s)}})\cdot g(V_{I_1(s)}, V_{I_2(s)})

其中，VI1(s)V_{I_1(s)}表示第一张图片的第s个block的特征，VI2(s)V_{I_2(s)}同理。CindI1(s)C_{ind_{I_1(s)}}和CindI2(s)C_{ind_{I_2(s)}}分别表示两个block的块索引所对应的聚类中心点。h(a,b)h(a,b)和g(a,b)g(a,b)分别代表两个相似度评价函数，如下：

h(CindI1(s),CindI2(s))=1m2∑exp⁡(−d(CindI1(s),CindI2(s)))=1m2∑1ed(⋅)g(VI1(s),VI2(s))=exp⁡(−d(VI1(s),VI2(s)))=1ed(⋅)h(C_{ind_{I_1(s)}}, C_{ind_{I_2(s)}})=\frac{1}{m^2}\sum\exp(-d(C_{ind_{I_1(s)}}, C_{ind_{I_2(s)}}))=\frac{1}{m^2}\sum\frac{1}{e^{d(\cdot)}} \\ g(V_{I_1(s)}, V_{I_2(s)})=\exp(-d(V_{I_1(s)}, V_{I_2(s)}))=\frac{1}{e^{d(\cdot)}}

其中，d(⋅)d(\cdot)表示二者之间的欧几里得距离，m即为我们在块索引一节选出的与之距离最近的m个聚类中心点的个数m。

s_score的取值范围应介于区间(0,1](0, 1]，分数越大，则两张图片的相似度也就越高。

随着两个block相似度的提高，两个block应该被划分到聚类中心点集的交集也就会随之增多，点集之间的欧几里得距离也就会随之减小并趋向于0，则计算公式左边的部分h(⋅)h(\cdot)将随之增大并趋向于1。同理，两个block的组合描述子特征之间的欧几里得距离也将趋向于0，公式右边的g(⋅)g(\cdot)的值也将随之增大并趋向于1。因此对于整体来说，相似度越高，s_score的得分越大。

同时，我们还可以给组合特征V(s)SCV_{(s)}^{SC}和深度特征V(s)CNNV_{(s)}^{CNN}之间加上一个对最终相似度得分计算的影响权重，这两个权重则即为μ1\mu_1和μ2\mu_2，其需要遵循μ1+μ2=1\mu_1+\mu_2=1，由此我们可以得到b_score的计算公式，如下所示：

b_score=μ1×s_score(V(s)SC)+μ2×s_score(V(s)CNN)\text{b\_score}=\mu_1\times\text{s\_score}(V_{(s)}^{SC})+\mu_2\times\text{s\_score}(V_{(s)}^{CNN})

最终，我们对一张图像所切分出来的S个block的相似性求和，即可得到两张图像之间的相似性，我们将其即为score，公式如下：

score=∑b_score\text{score}=\sum\text{b\_score}

0x04 Block-based Image Matching (BBIM) Algorithm

离线过程

  1. 在训练数据集上依据所有图片所有block的SURFCN描述子训练码表，并采用VLAD算法将其编码，记为：CvladSCC_{vlad}^{SC}
  2. 把一张图片I分成S个block
  3. 提取每一个block的SURF描述子
  4. 围着上一步提取的SURF描述子，提取以其为中心的一个近邻矩阵内的CN描述子
  5. 组合SURF描述子和CN描述子，组合描述子又称为SURFCN (SC)描述子
  6. 对每一个block的组合描述子，使用VLAD算法编码为一个向量V(s)SCV^{SC}_{(s)}
  7. 提取每个block的深度特征，记为V(s)CNNV^{CNN}_{(s)}
  8. 在待检索的图像数据集上基于VSCV^{SC}和VCNNV^{CNN}分别训练一个码表，记为CSCC^{SC}和CCNNC^{CNN}
  9. 为每一个block依据组合描述子特征和深度特征创建一个块索引，记为ind(s)SCind_{(s)}^{SC}和ind(s)CNNind_{(s)}^{CNN}

检索过程

  1. 将待检索的图片Q分为S个block
  2. 提取每一个block的SURF描述子CN描述子，并将其组合为SURFCN描述子
  3. 对每一个block s的SURFCN描述子进行VLAD编码，得向量V(s)SCV^{SC}_{(s)}
  4. 提取每个block的深度特征，记为V(s)CNNV^{CNN}_{(s)}
  5. 对每一个block依据离线过程中训练的码表CSCC^{SC}和CCNNC^{CNN}计算出其块索引向量
  6. 计算此图片与待检索数据集中所有图片的相似性score
  7. 从数据集中返回前p张相似性得分最高的图片

0x04 实践论

作者在实践过程中，对图像提取的是dense SURF descriptors，并在以每一个描述子为中心的周围一个4x4的矩阵内提取的CN描述子。作者在A数据内预训练一个码表，然后使用B数据集内的图片作为待检索目标数据集以及检索数据集。对于深度特征的提取，作者选用的是VGG-f模型，抽取其第二个全连接层的输出，输出为一个4096维的向量的。

对于组合描述子计算中的SURF描述子和CN描述子所占权重问题，作者进行了探究。发现在holidays数据集上，ω1=ω2=0.5\omega_1=\omega_2=0.5时，检索的mAP最高，最高为0.7373。但是在Oxford5K数据集上，由于大部分建筑物的颜色特征都差不多，导致CN描述子在不相似图片上的区分度并不高，继而导致当取值ω1=ω2=0.5\omega_1=\omega_2=0.5时，并不能取得最好的检索效果。经试验得知，在Oxford5K数据集上，取值ω1=0.9,ω2=0.1\omega_1=0.9, \omega_2=0.1时，检索效果最好，mAP最高为0.3899。

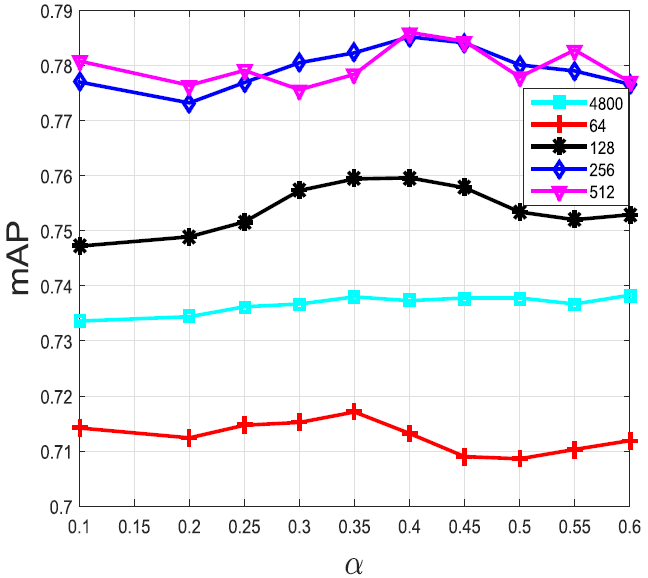
作者同样对在进行VLAD编码过程中，进行power-law normalization时的常量α\alpha的选取对检索结果的影响做了探究，发现最佳的α\alpha取值应介于0.1-0.6之间。VLAD编码出来原始向量有4800维，作者同样对使用PCA算法对原始VLAD向量进行降维和白化对其mAP的影响做了探究。在Holidays数据集中的结果如下图所示：

其中每条不同的线后面的数字为使用PCA算法降维后的维度，4800为原始向量。

作者还对计算b_score时，组合特征和深度特征的s_score的权重μ1\mu_1和μ2\mu_2对检索mAP的影响做了探究。在Holidays数据集上的测试结果是，当依据SURFCN描述子预训练的码表的大小（聚类中心的个数）为64时，μ1\mu_1和μ2\mu_2的值均为0.5时，检索的mAP最好，最高为0.8261。

在进行检索的过程中，作者发现，有一些图片的block可能没有特征可以提取，对于这样的block将会在检索过程中被丢弃。用于VLAD编码SURFCN特征所训练的码表大小为64，用于建立块索引时所训练的码表大小为2048。在Holidays数据集中，如果单纯地将图片分块后使用VLAD编码后的SURFCN描述子进行检索，mAP为0.7579，如果单纯地使用深度特征进行检索，mAP为0.7885。如果将两个特征按前文所述方法进行组合，然后使用组合特征进行检索，mAP为0.8351。