评价体系

聚/分类算法

我们先来明确一个基本的概念，什么是聚类（Clustering）和什么是分类（Classification or Categorization）。

首先，二者最大的区别就是聚类是无标签的，而分类是有标签的。换句话说，聚类没有一个初始的客观的判断对错的标准，而分类是有一个初始的判断对错的标准的。分类是向事物分配标签，而聚类是将相似的事物放在一起。

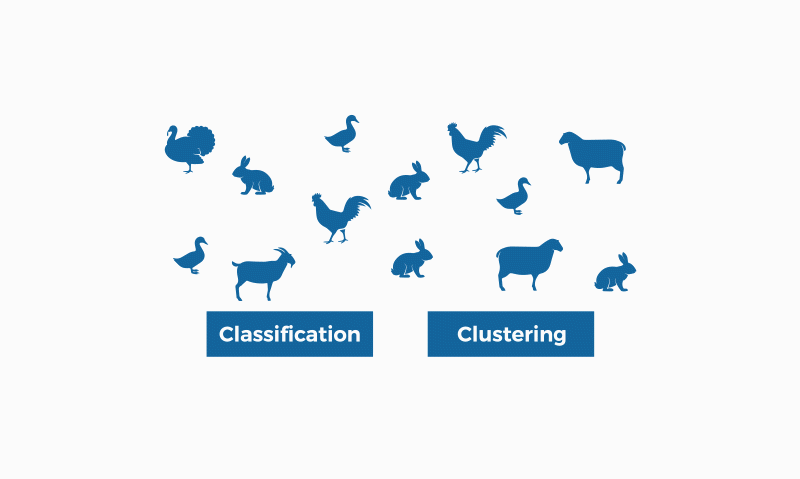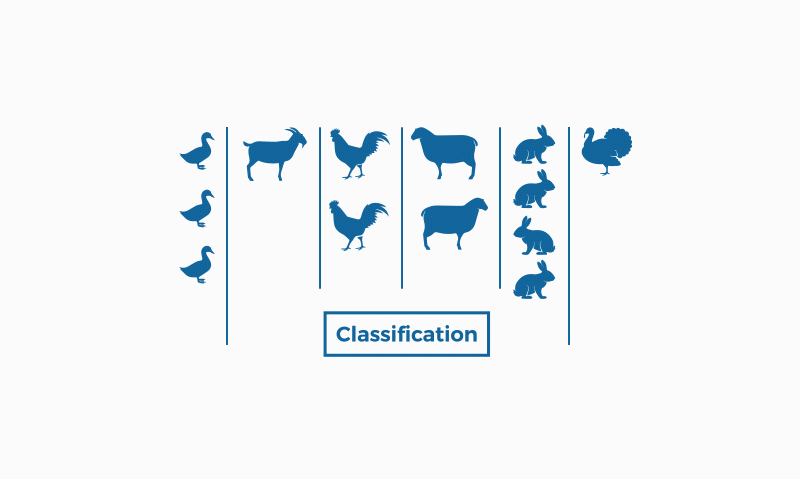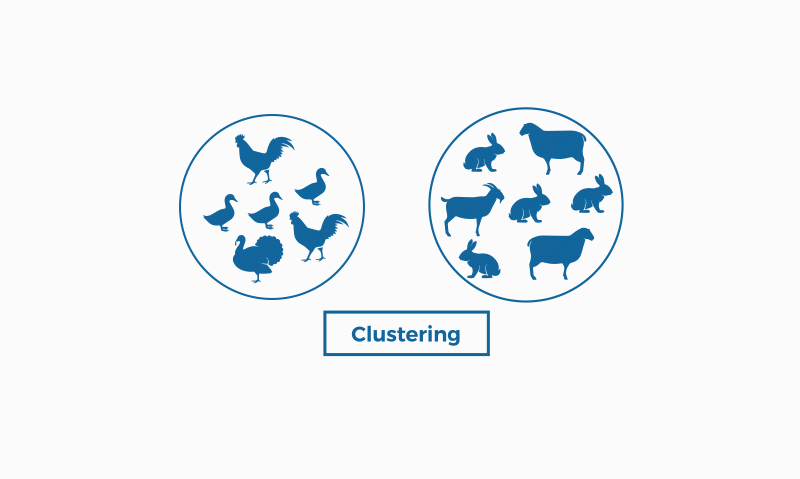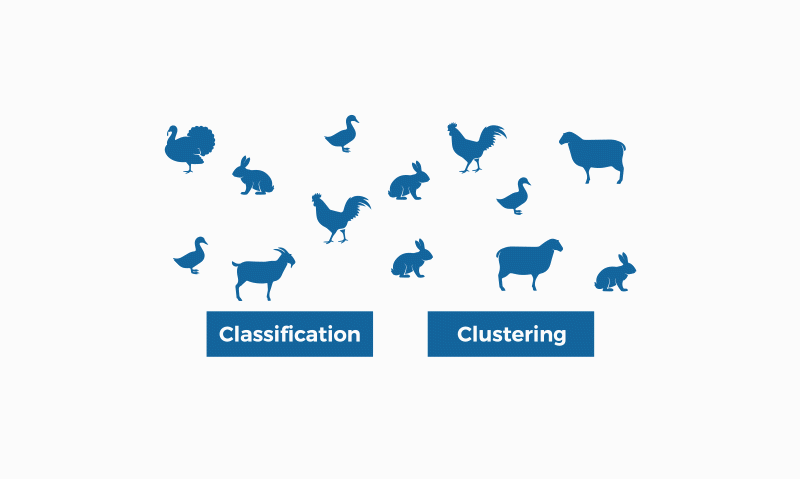
如下图，分类就是有给定的标签，有一定的客观事实作为依据，我开局就给分类引擎一个带有标签的训练集，告诉它什么样的是鸡，什么样的是狗，什么样的是其他动物，然后他就会对这些动物进行分类，对于分类的结果，鸡是鸡，狗是狗，狗的图片分到鸡的那一类下，那就是不对，那就是错的。

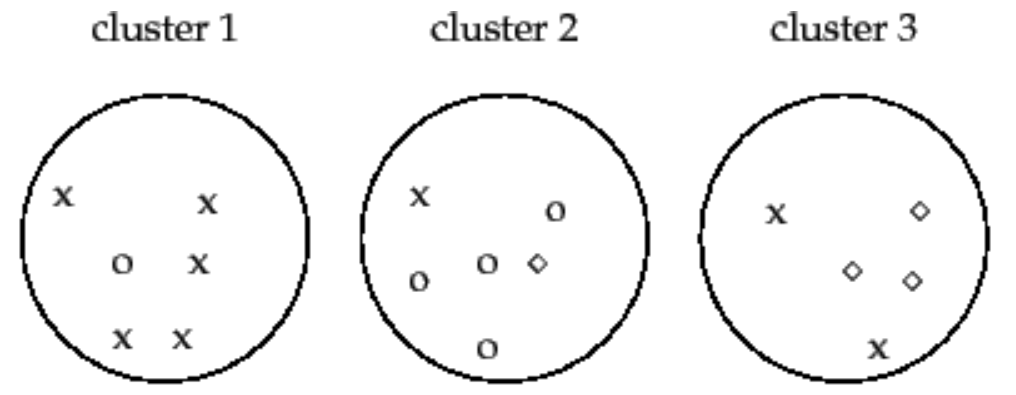
而聚类是无标签的，我开局就给聚类引擎一些没有标签的数据集，告诉它这是一堆动物的图片，你想办法给我从中找出他们之间的共性来，并按照相似的共性给我分成K类。如下图所示的聚类算法就是按照左边是2条腿的动物，右边是4条腿的动物进行聚类，这是对的，同样，如果按照动物头上有没有角进行聚类，也是对的。因为没有初始给定的判断结果对错的标准。

亦因如此，聚类是无监督的学习，分类是有监督的学习。

聚类前

聚类前的任务是评价数据集是否适合聚类。

Hopkins Statistic

霍普金斯统计量（Hopkins Statistic）用于评估给定的数据集是否存在有意义的可聚类的非随机结构。如果一个数据集是随机均匀的点生成的，虽然也可以产生聚类结果，但是聚类的结果没有意义。聚类的前提需要数据是非均匀分布的。霍普金斯统计量的值在区间[0, 1]之间，[0.01, 0.3]表示数据结构regularly spaced，该值为0.5时数据是均匀分布的，[0.7, 1]表示聚类趋势很强，值越高表示聚类趋势越强。其算法流程如下：

首先在空间D中进行均匀取样，得到n个点，记作$p_1, p_2, p_3\cdots p_n$，然后分别找出这n个点在空间D中距离最近的点（欧几里得距离即可），将其之间的距离记作$x_1, x_2, x_3\cdots x_n$。即：

$$x_i=\min_{v\in D}(\text{distance}(p_i, v_i))$$

然后从样本可能的取值空间中随机生成n个服从均匀分布的点，记作$q_1, q_2, q_3\cdots q_n$，对于随机生成的点，找到一个离它最近的样本点，将其之间的距离记作$y_1, y_2, y_3\cdots y_n$。即：

$$y_i=\min_{v\in D}(\text{distance}(q_i, v_i))$$

则霍普金斯统计量则可表示为：

$$\text{H}=\frac{\sum_{i=1}^ny_i}{\sum_{i=1}^nx_i+\sum_{i=1}^ny_i}$$

如果D接近均匀分布，，则$\sum_{i=1}^nx_i$和$\sum_{i=1}^ny_i$将会很接近，H大约为0.5，如果D是高度倾斜的，则$\sum_{i=1}^nx_i$将会显著小于$\sum_{i=1}^ny_i$，H的值将接近于1。H的值大于0.75则在90%的置信度（confidence level）下其具有良好的聚类趋势（clustering tendency）。

参考资料：

Assessing Clustering Tendency

聚/分类后

无标签的聚类

Normalized Mutual Information

Normalized Mutual Information (NMI)，是一个用于衡量聚类的质量与所聚类类别的个数之间的关系的指标，用于度量两个聚类结果的相近程度。

Silhouette Coefficient

Silhouette Coefficient主要用来衡量对于相同的原始数据集，不同的聚类算法或者同一算法的不同运行方式对聚类结果产生的影响，判断聚类是否合理、有效。

算法流程如下：

计算样本$i$到同簇其它样本的平均距离，记作$a(i)$，$a(i)$越小，说明样本$i$越应该被聚到此类。将$a(i)$称作样本$i$的簇内不相似度。

计算样本$i$到某簇$C_j$内的所有样本的平均距离，记作$b_{ij}$，称作样本$i$与簇$C_j$的不相似度。定义样本$i$的簇间不相似度为$b_i=\min\{b_{i1},b_{i2},\cdots,b_{ik}\}$

此后，对于样本$i$的Silhouette Coefficient即为：

$$s(i)=\frac{b(i)-a(i)}{\max\{a(i),b(i)\}}$$

若$s(i)$接近1，说明样本$i$聚类合理，若$s(i)$接近-1，则说明样本$i$更应该被分类到其它的簇，若$s(i)$接近于0，则说明样本$i$在两个簇的边界上。

Calinski-Harabasz Index

聚类算法的最终目的是要做到类别内部数据的协方差越小越好，类别之间的协方差越大越好。聚类效果越好，Calinski-Harabasz Index（CH系数）的值会高。其值可以表示为：

$$s(k)=\frac{tr(B_k)}{tr(W_k)}\frac{m-k}{k-1}$$

其中tr表示矩阵的迹，$B_k$表示类别之间的协方差矩阵，$W_k$表示内部数据的协方差矩阵，m为训练集的样本数，k为所划分的类别数。

同时适用

Purity/Precision

当有标签的时候，就是Precision，精度。分类的精度就是分类正确的个数除以分类总体样本的个数。

当没有标签的时候呢，就是Purity，纯度。聚类的纯度就是将所各聚类类别中数量最多的那一项作为当前类的正确结果，然后用所有类别中正确的数量除以样本的总数。

对于聚类算法来说，纯度的最小值为：

$$假设分为k类，共有n个点\\ 那么平均一组里面有\frac{n}{k}个样本\\ 作为正确标签的最大的那一个最少占\frac{n}{k^2}+1个\\ 对于这一组而言的最低纯度值为：\frac{\frac{n}{k^2}+1}{\frac{n}{k}}=\frac{\frac{n}{k}+k}{n}=\frac{n+k^2}{nk}=\frac{1}{k}+\frac{k}{n}\\ 把1360个样本分成11组，最低纯度值为：\frac{1}{11}+\frac{11}{1360}\approx0.0990=9.90\%$$